Última actualización: enero 30, 2022
5.0. Introducción
5.0.1. ¿Por qué debería tomar este módulo?
¡Bienvenido a sistemas de numeración!
¿Adivinen qué? Esta es una dirección IPv4 de 32 bits de un equipo en una red: 11000000.10101000.00001010.00001010. Se muestra en binario. Esta es la dirección IPv4 del mismo equipo en decimal punteado: 192.168.10.10. ¿Con cuál prefieres trabajar? Las direcciones IPv6 son 128 bits. Para que estas direcciones sean más manejables, IPv6 utiliza un sistema hexadecimal de 0-9 y las letras A-F.
Como administrador de red, debe saber cómo convertir direcciones binarias en decimales punteados y decimales punteados en binarias. También necesitará saber cómo convertir decimal punteado en hexadecimal y viceversa. (Sugerencia: Todavía necesita sus habilidades de conversión binaria para que esto funcione).
Sorprendentemente, no es tan difícil cuando aprendes algunos trucos. Este módulo contiene una actividad llamada el juego binario que realmente le ayudará a comenzar. Entonces, ¿por qué esperar?
5.0.2. ¿Qué aprenderá en este módulo?
Título del módulo: Sistemas numéricos
Objetivos del módulo: Calcule los números entre los sistemas decimales, binarios y hexadecimales.
| Título del tema | Objetivo del tema |
|---|---|
| Sistema de numeración binaria | Calcule los números entre los sistemas decimales y binarios. |
| Sistema numérico hexadecimal | Calcule los números entre los sistemas decimales y hexadecimales. |
5.1. Sistema de numeración binaria
5.1.1. Direcciones binarias e IPv4
Las direcciones IPv4 comienzan como binarias, una serie de solo 1 y 0. Estos son difíciles de administrar, por lo que los administradores de red deben convertirlos a decimales. En este tema se muestran algunas formas de hacerlo.
Binario es un sistema de numeración que consta de los dígitos 0 y 1 llamados bits. En contraste, el sistema de numeración decimal consta de 10 dígitos que consisten en los dígitos desde el 0 al 9.
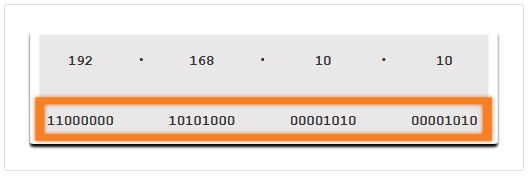
Es importante que comprendamos el sistema binario, ya que los hosts, los servidores y los dispositivos de red usan el direccionamiento binario. Específicamente, usan direcciones IPv4 binarias, como se muestra en la figura, para identificarse entre sí.
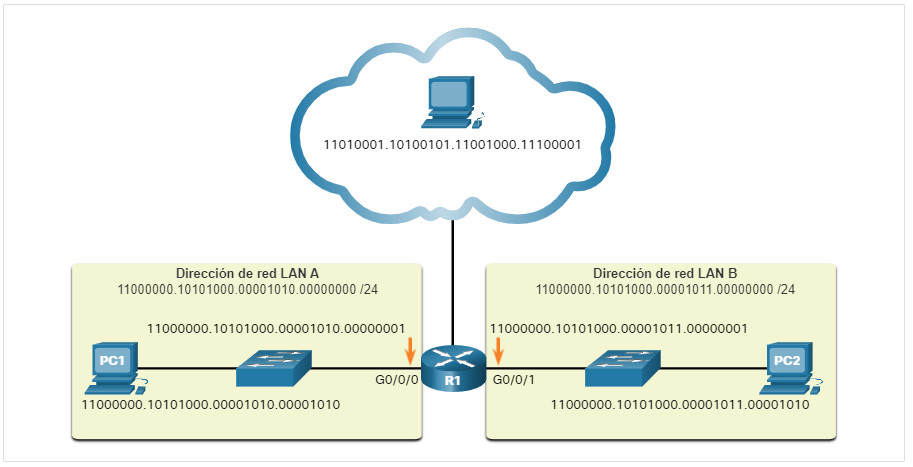
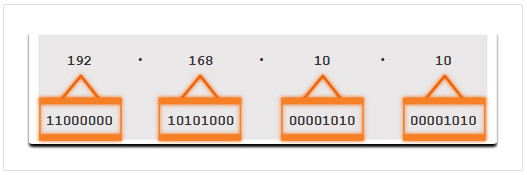
Cada dirección consta de una cadena de 32 bits, divididos en cuatro secciones denominadas octetos. Cada octeto contiene 8 bits (o 1 byte) separados por un punto. Por ejemplo, a la PC1 de la ilustración se le asignó la dirección IPv4 11000000.10101000.00001010.00001010. La dirección de gateway predeterminado sería la de la interfaz Gigabit Ethernet del R1, 11000000.10101000.00001010.00000001.
Binario funciona bien con hosts y dispositivos de red. Sin embargo, es muy difícil para los humanos trabajar con ellos.
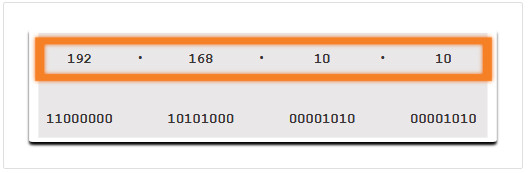
Para facilitar el uso por parte de las personas, las direcciones IPv4 se expresan comúnmente en notación decimal con puntos. A la PC1 se le asigna la dirección IPv4 192.168.10.10, y su dirección de puerta de enlace predeterminada es 192.168.10.1, como se muestra en la figura.
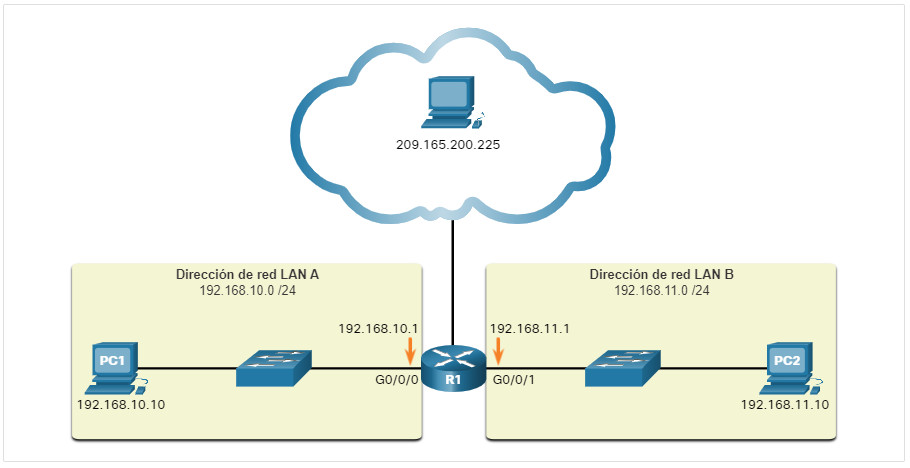
Para tener una buena comprensión del direccionamiento de red, es necesario comprender el direccionamiento binario y obtener habilidades prácticas en la conversión entre direcciones IPv4 binarias y decimales punteadas. Esta sección cubrirá cómo convertir entre sistemas de numeración de base dos (binario) y base 10 (decimal).
5.1.2. Video – Conversión entre sistemas de numeración binarios y decimales
Haga clic en reproducir en la figura para ver un video que muestra cómo convertir entre sistemas de numeración binarios y decimales.
5.1.3. Notación de posición binaria
Para aprender a convertir de sistema binario a decimal, es necesario entender la notación de posición. El término «notación de posición» significa que un dígito representa diferentes valores según la «posición» que el dígito ocupa en la secuencia de números. Ya conoce el sistema de numeración más común, el sistema de notación decimal (de base 10).
El sistema de notación posicional decimal funciona como se describe en la tabla.
| Radix | 10 | 10 | 10 | 10 |
|---|---|---|---|---|
| Posición en número | 3 | 2 | 1 | 0 |
| Cálculo | (103) | (102) | (101) | (100) |
| Valor de la posición | 1000 | 100 | 10 | 1 |
Las viñetas siguientes describen cada fila de la tabla.
- Fila 1, Radix es la base numérica. La notación decimal se basa en 10, por lo tanto, la raíz es 10.
- Fila 2, Posición en número considera la posición del número decimal que comienza con, de derecha a izquierda, 0 (1ª posición), 1 (2ª posición), 2 (3ª posición), 3 (4ª posición). Estos números también representan el valor exponencial utilizado para calcular el valor posicional en la cuarta fila.
- Fila 3 calcula el valor posicional tomando la raíz y elevándola por el valor exponencial de su posición en la fila 2.
Nota: n0 es = 1. - El valor posicional de la fila 4 representa unidades de miles, cientos, decenas y unos.
Para usar el sistema de posición, una un número dado con su valor de posición. El ejemplo en la tabla ilustra cómo se usa la notación posicional con el número decimal 1234.
| Millares | Centenas | Decenas | Unidades | |
|---|---|---|---|---|
| Valor de posición | 1000 | 100 | 10 | 1 |
| Número decimal (1234) | 1 | 2 | 3 | 4 |
| Cálculo | 1 x 1000 | 2 x 100 | 3 x 10 | 4 x 1 |
| Add them up… | 1000 | + 200 | + 30 | + 4 |
| Resultado | 1,234 | |||
En contraste, la notación posicional binaria opera como se describe en la tabla.
| Radix | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
|---|---|---|---|---|---|---|---|---|
| Posición en número | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Cálculo | (27) | (26) | (25) | (24) | (23) | (22) | (21) | (20) |
| Valor de la posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Las viñetas siguientes describen cada fila de la tabla.
- Fila 1, Radix es la base numérica. La notación binaria se basa en 2, por lo tanto, el radix es 2.
- Fila 2, Posición en número considera la posición del número binario que comienza con, de derecha a izquierda, 0 (1ª posición), 1 (2ª posición), 2 (3ª posición), 3 (4ª posición). Estos números también representan el valor exponencial utilizado para calcular el valor posicional en la cuarta fila.
- Fila 3 calcula el valor posicional tomando la raíz y elevándola por el valor exponencial de su posición en la fila 2.
Nota: n0 es = 1. - El valor posicional de la fila 4 representa unidades de uno, dos, cuatro, ocho, etc.
El ejemplo en la tabla ilustra cómo un número binario 11000000 corresponde al número 192. Si el número binario fuera 10101000, el número decimal correspondiente sería 168.
| Valor de posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Número binario (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cálculo | 1 x 128 | 1 x 64 | 0 x 32 | 0 x 16 | 0 x 8 | 0 x 4 | 0 x 2 | 0 x 1 |
| Añádanlos.. | 128 | + 64 | +0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Resultado | 192 | |||||||
5.1.5. Convertir binario a decimal
Para convertir una dirección IPv4 binaria a su equivalente decimal punteada, divida la dirección IPv4 en cuatro octetos de 8 bits. A continuación, aplique el valor de posición binario al primer octeto del número binario y calcule según corresponda.
Por ejemplo, suponga que 11000000.10101000.00001011.00001010 es la dirección IPv4 binaria de un host. Para convertir la dirección binaria a decimal, comience con el primer octeto, como se muestra en la tabla. Introduzca el número binario de 8 bits en el valor de posición de la fila 1 y, después, calcule para producir el número decimal 192. Este número entra en el primer octeto de la notación decimal punteada.
| Valor de posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Número binario (11000000) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cálculo | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Súmelos… | 128 | + 64 | + 0 | + 0 | + 0 | + 0 | + 0 | + 0 |
| Resultado | 192 | |||||||
A continuación, convertir el segundo octeto de 10101000 como se muestra en la tabla. El valor decimal resultante es 168 y entra en el segundo octeto.
| Valor de posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Número binario (10101000) | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| Cálculo | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Súmelos… | 128 | + 0 | + 32 | + 0 | + 8 | + 0 | + 0 | + 0 |
| Resultado | 168 | |||||||
Convertir el tercer octeto de 00001011 como se muestra en la tabla.
| Valor de posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Número binario (00001011) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Cálculo | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Súmelos… | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 1 |
| Resultado | 11 | |||||||
Convertir el cuarto octeto de 00001010 como se muestra en la tabla. Esto completa la dirección IP y produce 192.168.11.10.
| Valor de posición | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Número binario (00001010) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Cálculo | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Súmelos… | 0 | + 0 | + 0 | + 0 | + 8 | + 0 | + 2 | + 0 |
| Resultado | 10 | |||||||
5.1.7. Conversión de sistema decimal a binario
También es necesario comprender cómo convertir una dirección IPv4 decimal punteada a una binaria. La tabla de valores de posición binarios es una herramienta útil.
- 128
- 64
- 32
- 16
- 8
- 4
- 2
- 1
- Si no es, introduzca el binario 0 en el valor posicional 128.
- Si es, agregue un binario 1 en el valor posicional 128 y reste 128 del numero decimal.
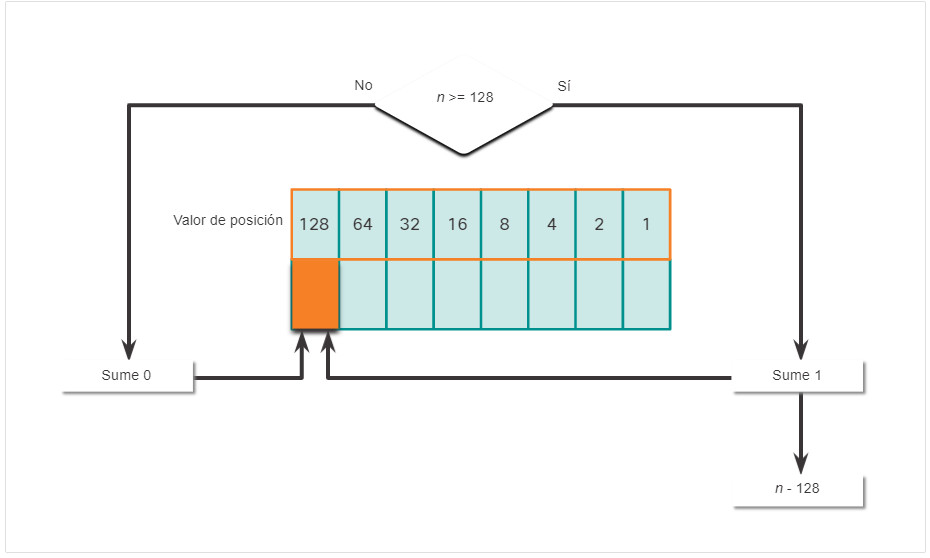
- Si no es, introduzca el binario 0 en el valor posicional 64.
- Si es, agregue un binario 1 en el valor posicional 64 y reste 64 del numero decimal.
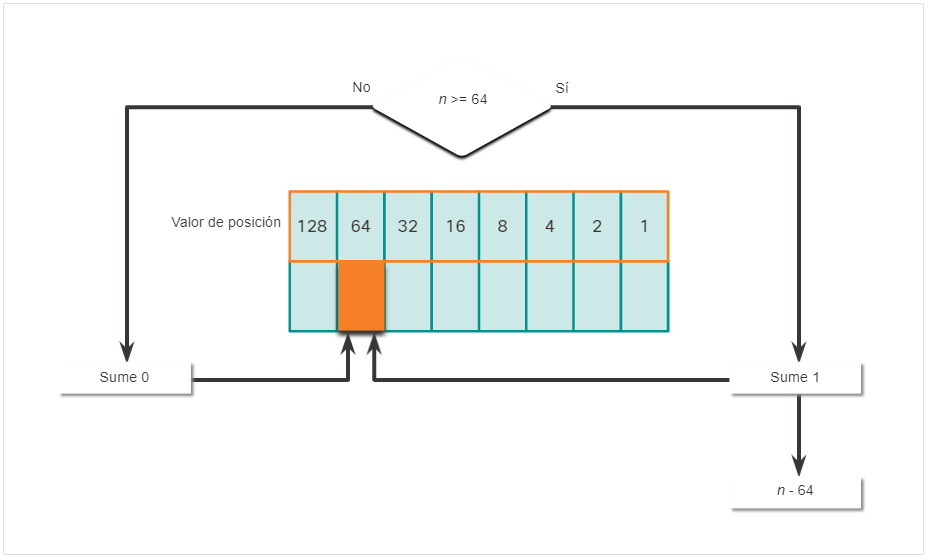
- Si no es, introduzca el binario 0 en el valor posicional 32.
- Si es, agregue un binario 1 en el valor posicional 32 y reste 32 del numero decimal.
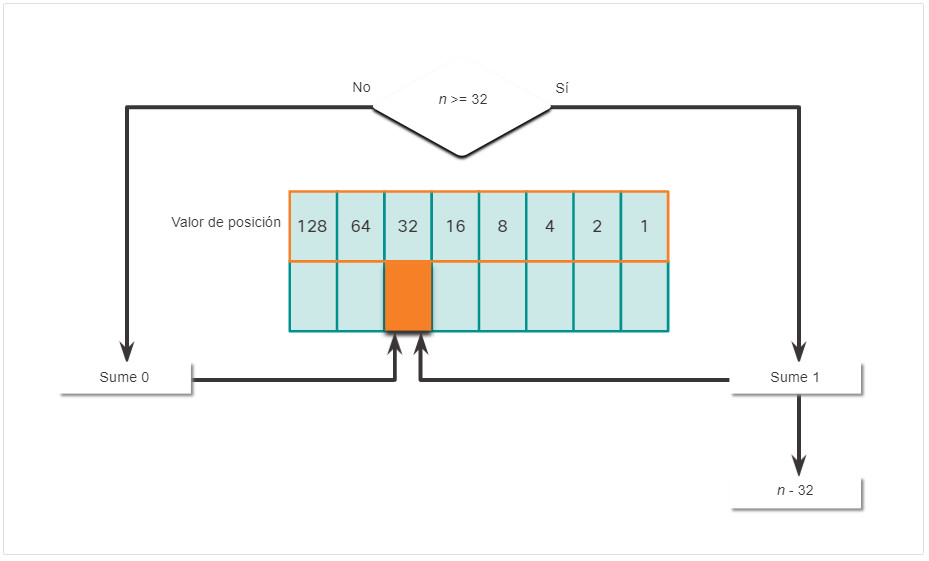
- Si no es, introduzca el binario 0 en el valor posicional 16.
- Si es, agregue un binario 1 en el valor posicional 16 y reste 16 del numero decimal.
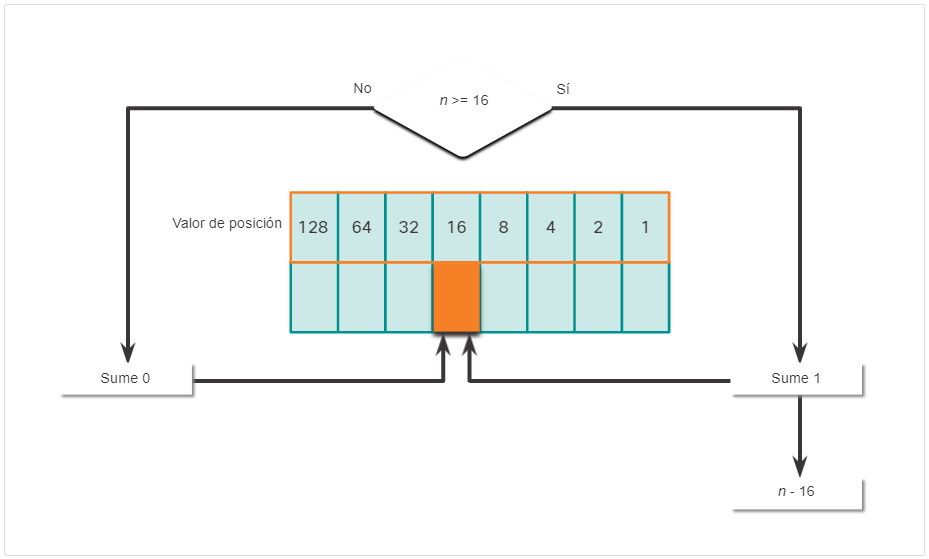
- Si no es, introduzca el binario 0 en el valor posicional 8.
- Si es, agregue un binario 1 en el valor posicional 8 y reste 8 del numero decimal.
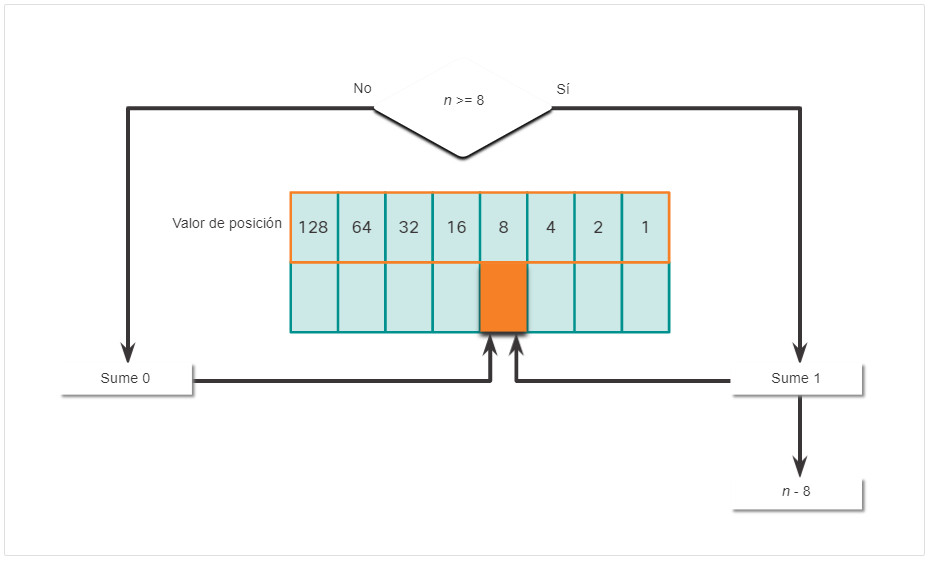
- Si no es, introduzca el binario 0 en el valor posicional 4.
- Si es, agregue un binario 1 en el valor posicional 4 y reste 4 del numero decimal.
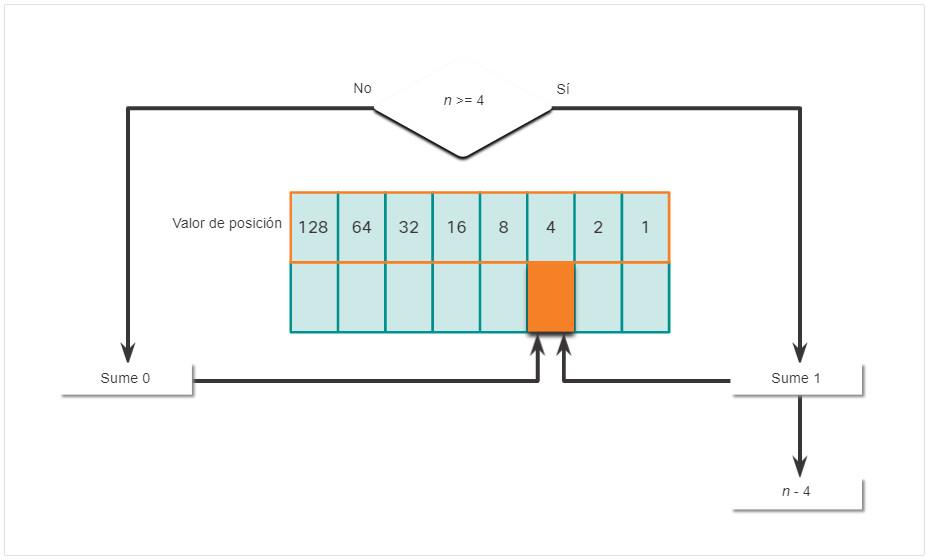
- Si no es, introduzca el binario 0 en el valor posicional 2.
- Si es, agregue un binario 1 en el valor posicional 2 y reste 2 del numero decimal.
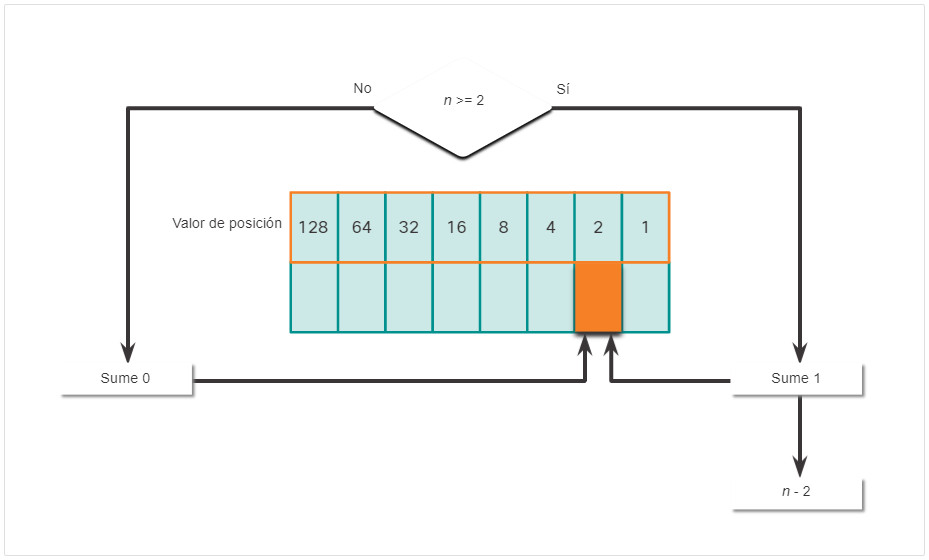
- Si no es, introduzca el binario 0 en el valor posicional 1.
- Si es, agregue un binario 1 en el valor posicional 1 y reste 1 del numero decimal.
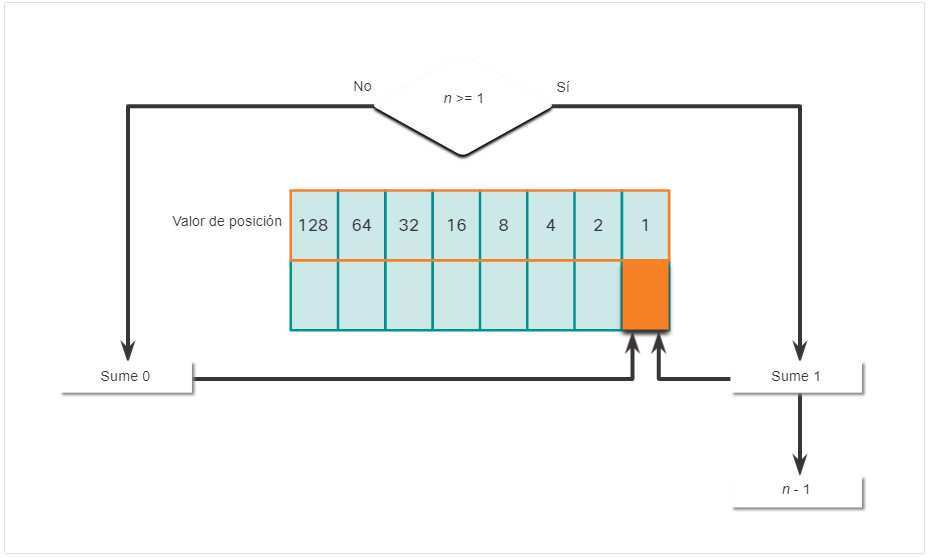
5.1.8. Ejemplo de conversión de sistema decimal a binario
Para poder comprender el proceso, considere la dirección IP 192.168.11.10.
El primer octeto número 192 se convierte a binario utilizando el proceso de notación posicional explicado anteriormente.
Es posible omitir el proceso de resta con números decimales menores o más pequeños. Por ejemplo, observe que es bastante fácil calcular el tercer octeto convertido a un número binario sin pasar realmente por el proceso de resta (8 + 2 = 10). El valor binario del tercer octeto es 00001010.
El cuarto octeto es 11 (8 + 2 + 1). El valor binario del cuarto octeto es 00001011.
La conversión de sistema binario a decimal puede parecer un desafío inicialmente, pero con la práctica resulta más fácil.
- Paso 1
- Paso 2
- Paso 3
- Paso 4
- Paso 5
- Paso 6
- Paso 7
- Paso 8
- Paso 9
- Paso 10
- Paso 11
- Sí es, por lo tanto, añadir un 1 al valor posicional de orden alto a un representar 128.
- Resta 128 de 192 para producir un resto de 64.
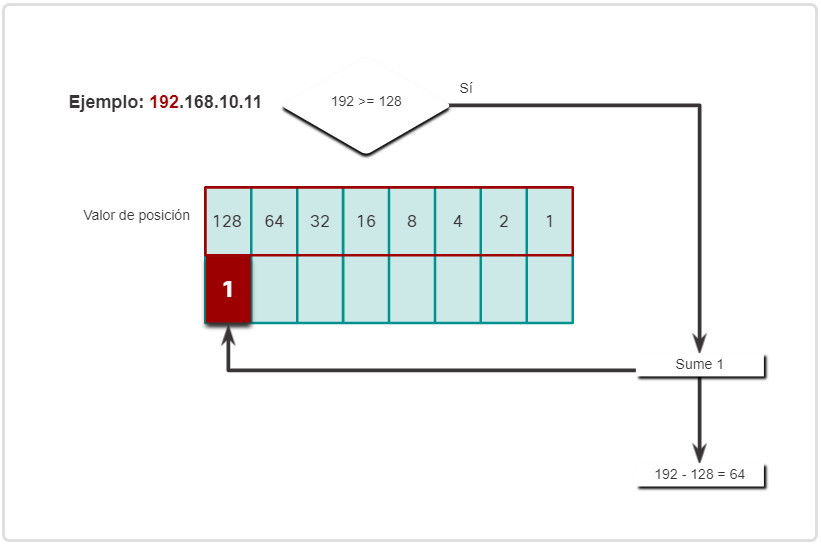
- Es igual, por lo tanto, agregue un 1 al siguiente valor posicional de alto orden.
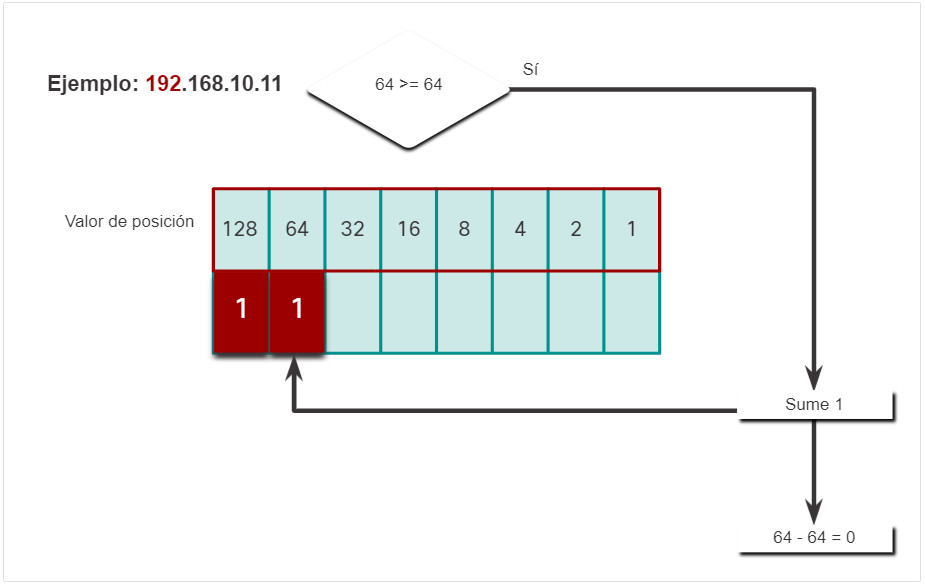
- El valor binario del primero octeto es 11000000.
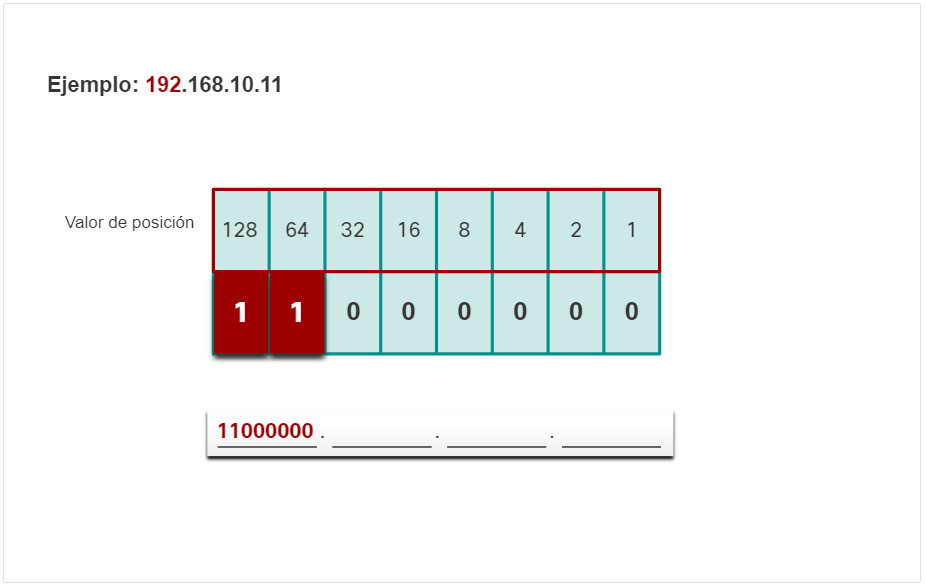
- Si, esto es cierto, por lo tanto agregue un 1 al valor posicional de alto orden para representar 128.
- Reste 128 de 168 para producir un resto de 40.
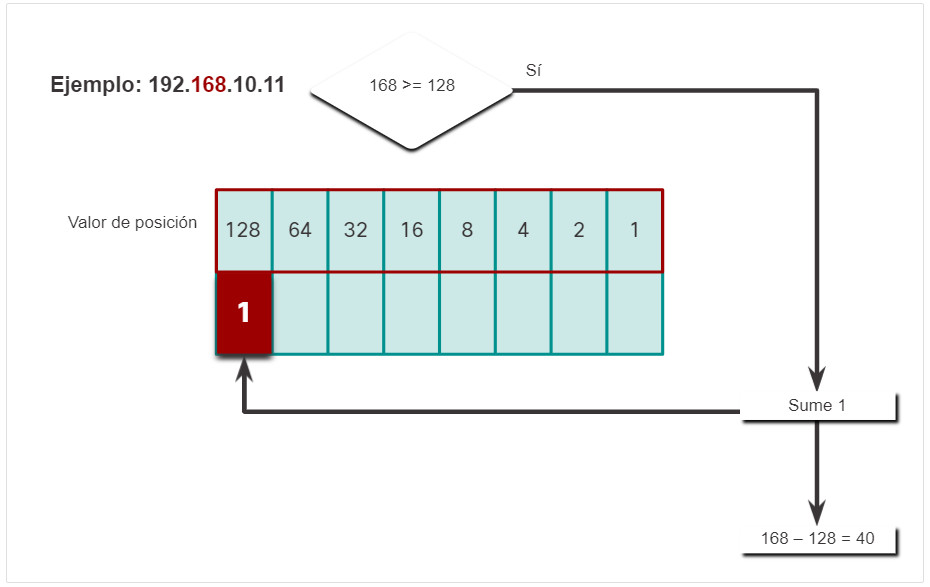
- No, no lo es, por lo tanto, ingrese un 0 binario en el valor posicional 64.
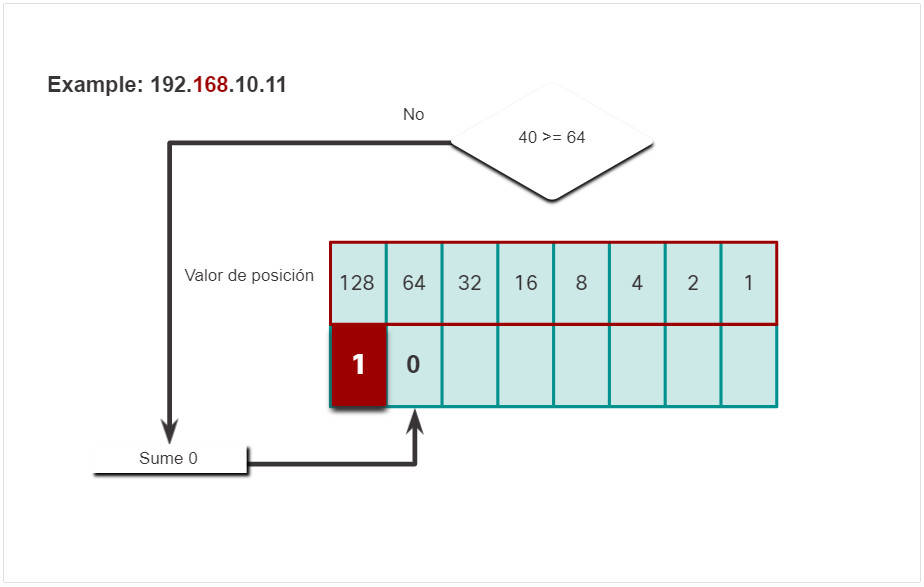
- Si, esto es cierto, por lo tanto agregue un 1 al valor posicional de alto orden para representar 32.
- Reste 32 de 40 para producir un resto de 8.
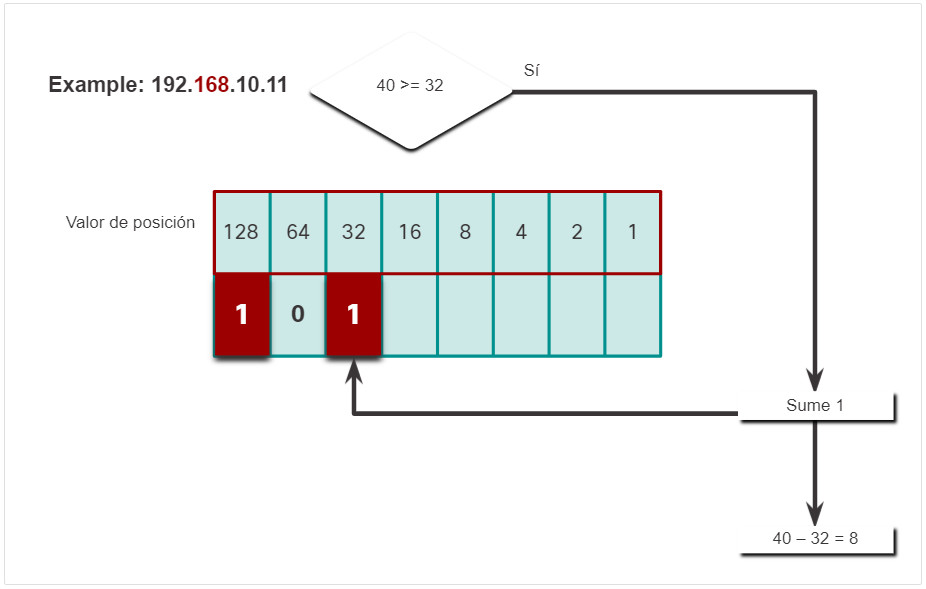
- No, no lo es, por lo tanto, introduzca un 0 binario en el valor posicional.
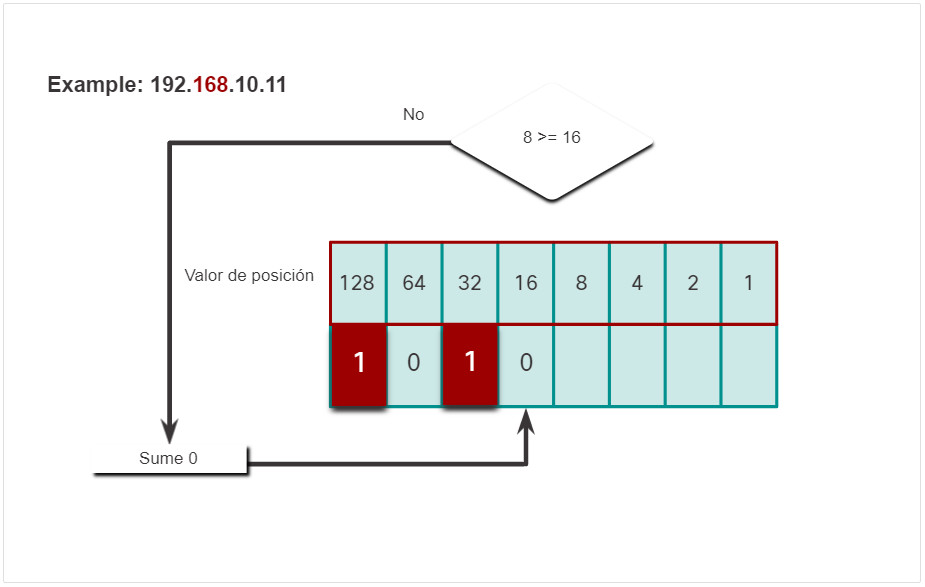
- Si, esto es cierto, por lo tanto agregue un 1.
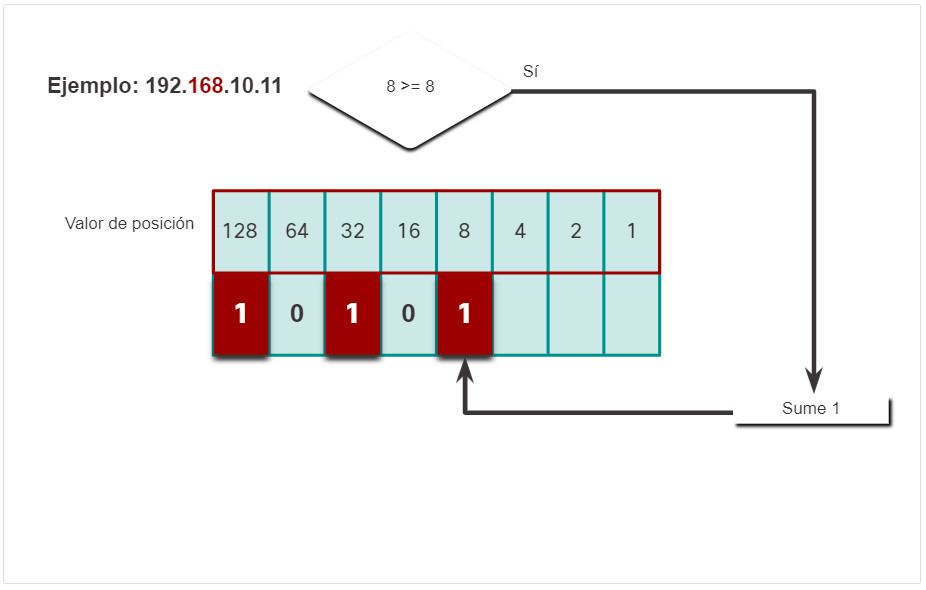
- El valor binario del segundo octeto es 10101000.
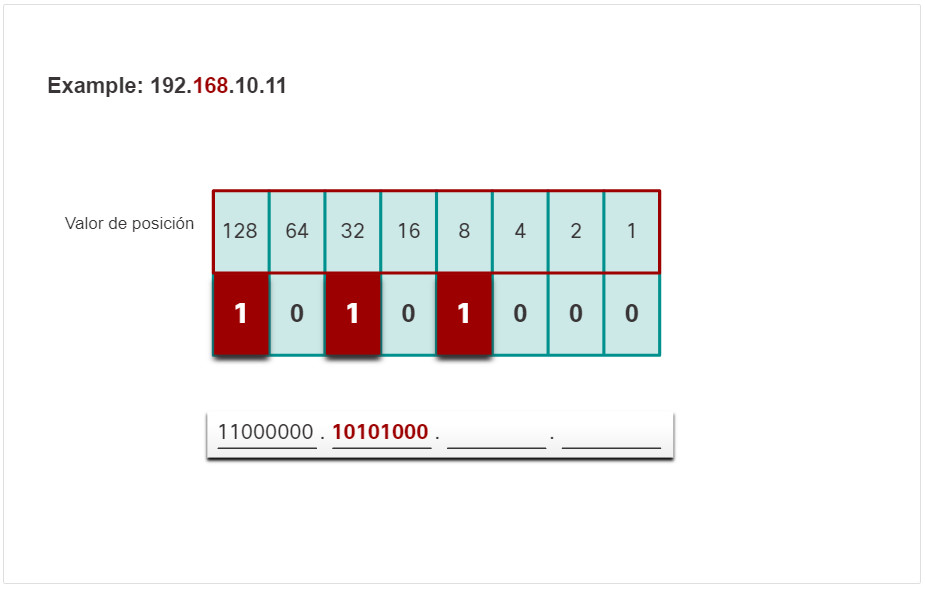
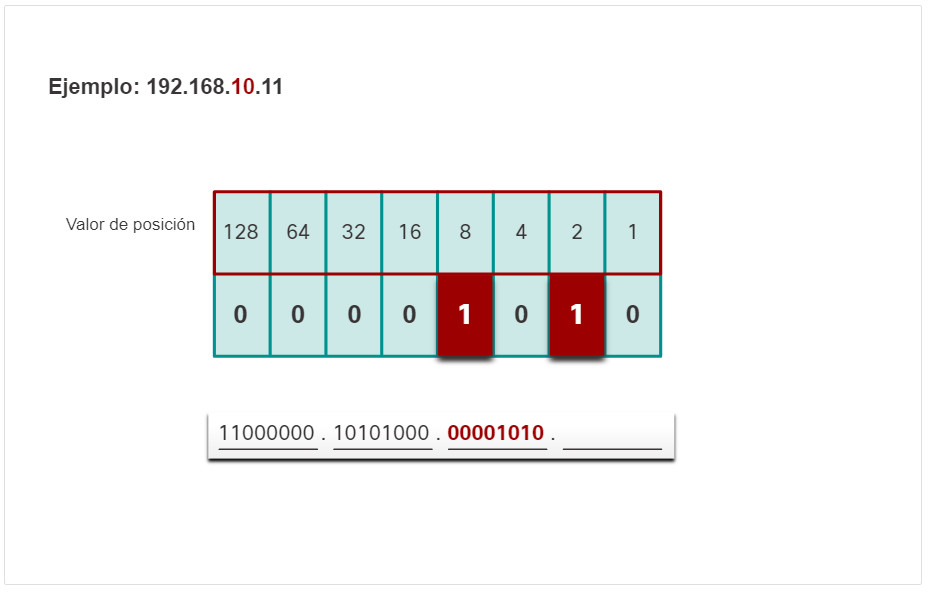

5.1.10. Actividad: Juego binario
Esta es una forma divertida de aprender números binarios para redes.
Link del juego: https://learningnetwork.cisco.com/docs/DOC-1803
Deberá iniciar sesión en cisco.com para utilizar este enlace. Será necesario crear una cuenta si aún no tiene una.
5.1.11. Direcciones IPv4
Como se mencionó al principio de este tema, los routers y las computadoras solo entienden binario, mientras que los humanos trabajan en decimal. Es importante que usted conozca a fondo estos dos sistemas de numeración y cómo se utilizan en redes.
- Dirección en formato decimal punteado
- Octetos
- Dirección de 32 bits
5.2. Sistema numérico hexadecimal
5.2.1. Direcciones hexadecimales e IPv6
Ahora sabes cómo convertir binario a decimal y decimal a binario. Necesita esa habilidad para comprender el direccionamiento IPv4 en su red. Pero es igual de probable que use direcciones IPv6 en su red. Para entender las direcciones IPv6, debe ser capaz de convertir hexadecimal a decimal y viceversa.
Así como el decimal es un sistema de base diez, el hexadecimal es un sistema de base dieciséis. El sistema base de dieciséis números usa los dígitos del 0 al 9 y las letras de la A a la F. La figura muestra los valores decimales y hexadecimales equivalentes para el binario 0000 a 1111.
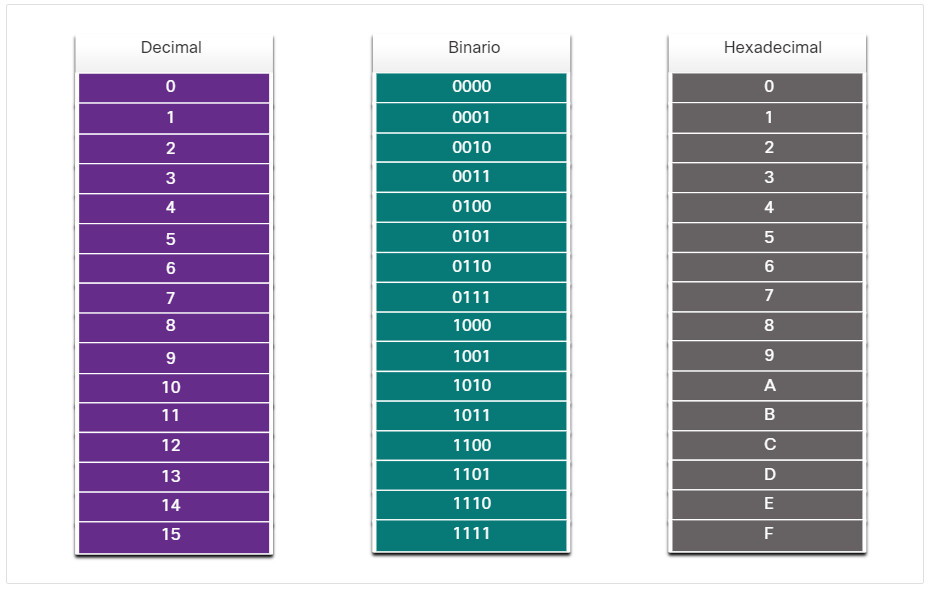
Binario y hexadecimal funcionan bien juntos porque es más fácil expresar un valor como un solo dígito hexadecimal que como cuatro bits binarios.
El sistema de numeración hexadecimal se usa en redes para representar direcciones IP Versión 6 y direcciones MAC Ethernet.
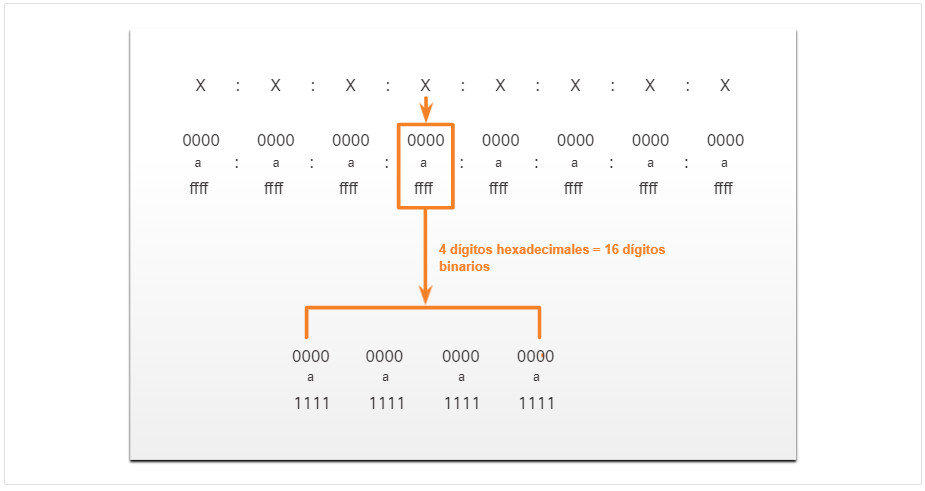
Las direcciones IPv6 tienen una longitud de 128 bits y cada 4 bits está representado por un solo dígito hexadecimal; para un total de 32 valores hexadecimales. Las direcciones IPv6 no distinguen entre mayúsculas y minúsculas, y pueden escribirse en minúsculas o en mayúsculas.
Como se muestra en la figura, el formato preferido para escribir una dirección IPv6 es x: x: x: x: x: x: x: x, donde cada «x» consta de cuatro valores hexadecimales. Al hacer referencia a 8 bits de una dirección IPv4, utilizamos el término “octeto”. En IPv6, un “hexteto” es el término no oficial que se utiliza para referirse a un segmento de 16 bits o cuatro valores hexadecimales. Cada “x” es un único hexteto, 16 bits o cuatro dígitos hexadecimales.
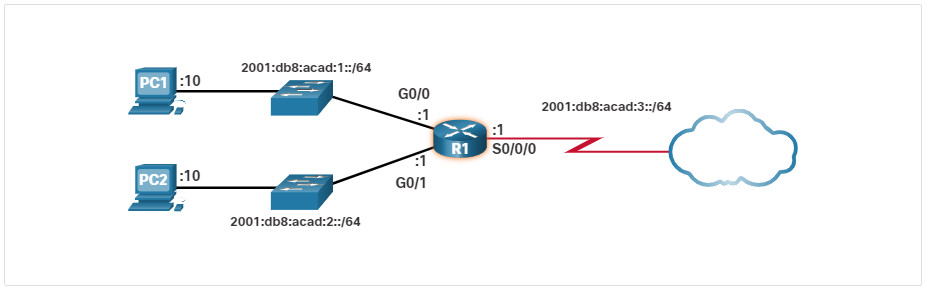
La topología de ejemplo de la figura muestra direcciones hexadecimales IPv6.
5.2.2. Video – Conversión entre sistemas de numeración hexadecimales y decimales
Haga clic en Reproducir en el vídeo para ver cómo convertir entre sistemas de numeración hexadecimal y decimal.
5.2.3. Conversiones decimales a hexadecimales
La conversión de números decimales a valores hexadecimales es sencilla. Siga los pasos indicados:
- Convertir el número decimal a cadenas binarias de 8 bits.
- Divida las cadenas binarias en grupos de cuatro comenzando desde la posición más a la derecha.
- Convierta cada cuatro números binarios en su dígito hexadecimal equivalente.
El ejemplo proporciona los pasos para convertir 168 a hexadecimal.
Por ejemplo, 168 convertido en hexadecimal usando el proceso de tres pasos.
- 168 en binario es 10101000.
- 10101000 en dos grupos de cuatro dígitos binarios es 1010 y 1000.
- 1010 es hex A y 1000 es hex 8.
Respuesta: 168 es A8 en hexadecimal.
5.2.4. Conversión hexadecimal a decimal
La conversión de números hexadecimales a valores decimales también es sencilla. Siga los pasos indicados:
- Convertir el número hexadecimal en cadenas binarias de 4 bits.
- Cree una agrupación binaria de 8 bits comenzando desde la posición más a la derecha.
- Convierta cada agrupación binaria de 8 bits en su dígito decimal equivalente.
En este ejemplo se proporcionan los pasos para convertir D2 a decimal.
- D2 en cadenas binarias de 4 bits es 1101 y 0010.
- 1101 y 0010 es 11010010 en un grupo de 8 bits.
- 11010010 en binario es equivalente a 210 en decimal.
Respuesta: D2 en hexadecimal es 210 en decimal.
5.3. Módulo de Práctica y Prueba
5.3.1. ¿Qué aprendió en este módulo?
Sistema númerico binario
El sistema binario es un sistema numérico que consiste en los números 0 y 1, denominados bits. En comparación, el sistema numérico decimal consiste en 10 dígitos, que incluyen los números 0 a 9. Es importante que comprendamos el binario porque los hosts, servidores y dispositivos de red usan direccionamiento binario, específicamente, direcciones binarias IPv4, para identificarse entre sí. Debe conocer el direccionamiento binario y cómo convertir entre direcciones IPv4 decimales binarias y con puntos. En este tema se presentan algunas formas de convertir decimal a binario y binario a decimal.
Sistema numérico hexadecimal
Así como el decimal es un sistema de base diez, el hexadecimal es un sistema de base dieciséis. El sistema de numeración hexadecimal utiliza los números 0 a 9 y las letras A a F. El sistema de numeración hexadecimal se utiliza en redes para representar direcciones IPv6 y direcciones MAC Ethernet. Las direcciones IPv6 tienen una longitud de 128 bits y cada 4 bits está representado por un solo dígito hexadecimal; para un total de 32 valores hexadecimales. Para convertir hexadecimal a decimal, primero debe convertir el hexadecimal a binario y, a continuación, convertir el binario a decimal. Para convertir decimal a hexadecimal, también debe convertir primero el decimal a binario.
